"Non, le virus SARS-CoV-2 ne contient pas des morceaux du VIH !"

«Non, le virus SARS-CoV-2 ne contient pas des morceaux du VIH !»

Le Pr Jean-Michel Claverie, spécialiste de génomique, revient sur les assertions du Pr Luc Montagnier concernant le caractère "fabriqué" du nouveau coronavirus. Il explique simplement pourquoi c’est impossible.

Kira Yan/iStock

Publié le 20.04.2020 à 11h00
Commenter

Par le Pr Jean-Michel Claverie

Dans plusieurs interviews récentes, le Pr Luc Montagnier a déclaré que le SARS-CoV-2 serait un virus manipulé par les Chinois et qui contiendrait de l'ADN de VIH (le virus du SIDA) ! Cette allégation reposerait sur la détection de similarités entre le génome du SARS-CoV-2 et celui du VIH.

Des séquences de « bases » désignées par des lettres

Les « textes » de ces génomes, écrits en une suite de « bases », désignées par des lettres (A, T, G, C), pour les deux virus, sont publiquement accessibles dans les bases de données publiques comme celle du National Institute for Biotechnology Information aux Etats-Unis.

Ces deux génomes, longs de 30.000 lettres (ou bases) pour le SARS-CoV-2 et de 9.200 lettres (ou bases) pour le VIH, codent, entre autres, pour les protéines qui permettent aux virus de se multiplier et de fabriquer les particules virales qui permettent leur dissémination.

Comment détecter une manipulation génétique ?

Grace aux méthodes du génie génétique, il est effectivement possible modifier les « textes » de tous les génomes, soit en modifiant une lettre à la fois, soit en y insérant l’équivalent de « paragraphes » (au moins 300 lettres) qui coderaient pour une protéine.

Pour détecter si une insertion a eu lieu, il s’agit de procéder comme on le ferait pour détecter un plagiat dans un roman : on regarde s’il n’y a pas, par endroit, des similarités un peu trop flagrantes, par exemple un paragraphe quasi-identique dans les deux textes.

Si cette similarité concerne seulement quelques mots, ou une phrase (par exemple une citation), on estimera qu’il n’y a pas eu d’emprunt d’un texte dans un autre. Pour que le plagiat soit caractérisé, il faut que l’étendue cette ressemblance dépasse la longueur communément admise pour une coïncidence entre deux textes écrits dans la même langue.

Comment comparer des génomes ?

La comparaison de deux génomes (pour détecter les éventuels emprunts de gènes de l’un vers l’autre) repose sur le même principe. Comme les génomes sont écrits avec les mêmes lettres ATGC, la détection d’une suite de lettres similaires n’est le signe d’un emprunt (une manipulation génétique) que si celle-ci est plus longue que ce que l’on attend des similarités restreintes qui peuvent être liées au hasard dans deux textes écrits totalement indépendamment.

Des méthodes universellement acceptées permettent :

- d’identifier facilement les zones de plus grande ressemblance entre les génomes du Cov-2 et du VIH

- de démontrer que leurs niveaux de similarité ne dépassent pas ce que l’on attend du hasard, et donc qu’elles ne constituent pas la preuve d’un emprunt (c’est-à-dire d’une insertion ou manipulation effectuée par des chercheurs).

Détection des similarités par calcul statistique.

La plus forte similarité détectée par la comparaison des 30.000 lettres du CoV-2 avec les 9.200 du VIH est une « phrase » de 38 lettres, dont 33 sont identiques, au prix d’une insertion (« - »):

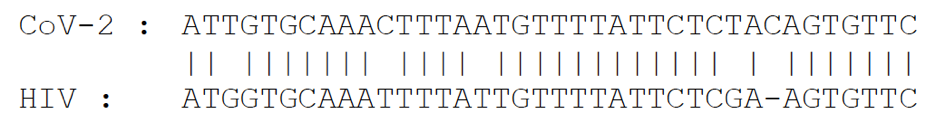
La seconde, moins bonne (28/30) est la suivante :

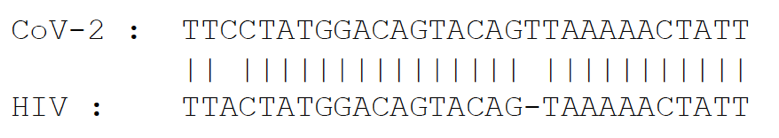
Un calcul (standard) des probabilités associé à ce type d’analyse nous indique que des zones atteignant ce niveau de similarité sont attendues plus de trois fois au hasard, c’est-à-dire en comparant des séquences de mêmes longueurs et de même composition en A,T,G et C fabriquées par un tirage aléatoire.

Conclusion : ces similarités ne sont en aucun cas inhabituelles, et ne peuvent pas servir d’argument en faveur d’une manipulation génétique qui aurait inséré un bout du génome VIH dans celui de SARS-CoV-2.

***Mais une autre* démonstration, *qui ne fait pas appel à un calcul statistique, est encore plus probante.***

Si l’on reprend maintenant le bout de séquence de SARS-CoV-2 qui aurait été emprunté au HIV (selon M. Montagnier) :

ATTGTGCAAACTTTAATGTTTTATTCTCTACAGTGTTC

et qu’on le cherche dans les textes des génomes d’autres souches de coronavirus bien plus anciennes (et naturellement associés aux chauves-souris), on peut vérifier qu’il est bien présent :

Exemple pour un virus isolé en 2005 (similarité 34/38):

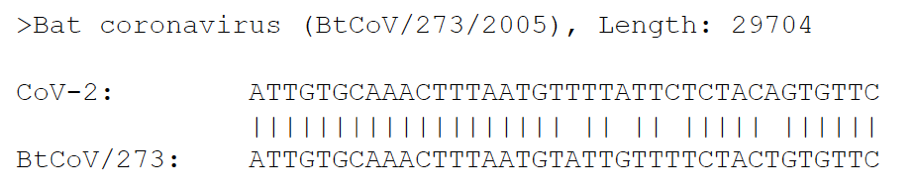
Cette zone de séquence code pour la séquence protéique « CANFNVLFSTVF » (les C, A, N …., lettres symbolisent différents acides aminés) conservée à l’identique dans toutes les souches de coronavirus car elle appartient à l’enzyme qui réplique le génome du virus (RNA polymerase) et dont la fonction lui est essentielle..

Conclusion, cette zone de ressemblance avec le VIH est fortuite, et existait dans la plupart des souches de coronavirus et ce, bien avant l’émergence de la Covid-19.

Dernier argument !

Enfin, si l’on se concentre sur la protéine du SARS-CoV-2 qui est la plus exposée à la surface du virus (la fameuse protéine « spike »), et qui serait donc la cible à privilégier pour faire un vaccin (car elle est la cible des anticorps) : sa comparaison détaillée avec la protéine d’enveloppe du virus VIH (la cible privilégiée pour faire un vaccin contre ce virus), à l’aide des méthodes universellement admises, ne détecte AUCUNE similarité.

Commentaires

FredericN
20.04.2020 19h55

Merci pour votre article très détaillé. J'aimerais revenir sur 2 contre arguments forts que vous avancez : - la probabilité qu'il y ait des séquences (33/38) et (28/30) est importante et donc normale (attendues plus de trois fois) - il y a déjà une séquence similaire sur BtCoV/273/2005. > Proba : en faisant les calculs, je ne retrouve pas votre résultat. En supposant tirage aléatoire des 4 lettres ACGT : La proba P1 d'avoir une chaine exacte de 38 lettres issues du VIH (9200 lettres) qui apparaisse sur la chaine Covid de 30000 lettres est approx de 3*10(-15). Si l'on considère qu'il y a 5 lettres erronées (33/38), on tombe à une proba P2 de moins de 1 chance sur 10 millions qu'une telle séquence puisse apparaitre. (détails : P1 = (30K-38) * (9.2K-38) * (1/4) exp38, et P2 = P1*1024*38*37*36*35/(5*4*3*2) ) (( Et la probabilité d'avoir les 2 chaines, approximativement et suivant le même calcul, est d'une chance sur 10 000 milliards. )) Je peux bien sûr me tromper, et aimerais avoir confirmation/infirmation de votre résultat. > Séquence similaire antérieure : Vous indiquez qu'il y a 1 séquence VIH qui apparait déjà ds coronavirus connu. Et de fait, vu le nbre de virus (bien supérieur aux 10 millions supra j'imagine), ce n'est pas choquant. Mais y a t il les 2 séquences VIH que vous citez ? La proba qu'il y ait la 2ème chaine sachant que la 1ère est en place est d'environ (même calcul que supra ajusté à 28/30) : aussi environ 1.5 chance sur 10 millions. (P2=(30K-30)*(9.2K-30)*1/4exp30*16*30*29/2 = 188*10+9*8.7*10-19 = 1.6*10-7) Et d'ailleurs y a t il d'autres séquences VIH communes entre VIH et Covid19 ? Merci encore de votre article et ds l'attente de vos éclairages Cordialement

Réagir
FredericN
20.04.2020 22h47

Question sur HIV apparaissant ds souche ancienne : en lisant https://www.biorxiv.org/content/10.1101/2020.02.13.945485v1.full.pdf p14, on voit que le BtCov/273/2005 que vous citez n'est pas ds la lignée génétique du Covid, mais du SARS. Est-ce que la séquence que vous indiquez apparait chez les prédecesseurs supposés du Covid ? Ou bien serait-elle apparue d'un coup chez lui ?

Réagir
- pourquoidocteur
  21.04.2020 13h18
  
  Cher FredericN : C’est un vrai plaisir d’avoir un lecteur aussi attentif. Comme j’aurais aimé vous avoir comme étudiant au premier rang de mes amphithéâtres ! Votre raisonnement est bon, sauf pour un détail qui change tout : nous sommes dans une situation de « tests multiples » dont il faut tenir compte par une correction (dite de Bonferroni). Un grand intérêt de votre réponse est de souligner la quantité d’information énorme que peut contenir un petit bout de séquence nucléique (d’où l’intérêt que lui porte la police scientifique). Une suite de 33 lettres (parmi A,T,G,C) peut engendrer 4^33 séquences différentes, soit 2^66 ou encore 64 x 10^18 (un pense bête : 2^10 = 1024 ≈ 10^3). La probabilité de tirer une de ces séquences au hasard, parmi toutes les séquences de longueur 33 possible est bien p1= 1/[64 x 10^18). Très faible donc. Mais nous devons maintenant nous engager dans de multiples corrections afin d’estimer une valeur plus réaliste de la probabilité d’avoir trouvé une de ces séquences de SARS-CoV-2 dans HIV. Toutes ces corrections sont nécessaires car nous n’avons pas précisé la séquence précise que nous cherchions AVANT de lancer nos comparaisons. La première correction est de nature combinatoire : nous avons 33 lettres identiques parmi les 38 essayées. Or il y a beaucoup de façon de tirer au hasard 33 lettres parmi 38. Cette valeur est donnée par la formule des combinaisons C(38, 33) ≈ 5x10^5 . La deuxième c’est que nous sommes partis du génome entier de SARS-CoV2 (30.000 nucléotides) qui contient approximativement 3 x 10^4 fragments successifs de 38 lettres, sur 2 brins (car le logiciel cherche aussi sur le brin complémentaire) soit 6x 10^4 fragments. Mais la troisième correction est encore plus importante, car la base de données des génomes de HIV contient plus de 100.000 séquences différentes, pour un total de 975 x 10^6 lettres (autant de positions d’alignements potentielles). Donc notre épreuve consiste à rechercher un alignement de n’importe quelle séquence de 33 lettres parmi 38 (p1=1/[64 x 10^18) en faisant N essais avec N= (5x10^5 )x(6x 10^4) x (975 x 10^6 ) ≈ 30 10^3 x (10^5x10^4x 10^6)= 30 x 10^18 La correction de Bonferroni consiste à simplement multiplier la probabilité p1 (un essai) par le nombre total d’essais. La probabilité du résultat (plus exactement l’espérance mathématique) obtenu est donc : 30 x 10^18 /(64 x 10^18) ≈ ½ Soit une chance sur deux d’obtenir le résultat observé. Notons enfin que ce résultat n’est obtenu que pour 2 souches différentes de HIV (isolats XJ16-6 et XJ47), parmi les 100.000 séquences testées dans la base de données! C’est un autre argument pour ne voir dans ce résultat que le hasard. Enfin, pour répondre à votre deuxième remarque, les deux régions de similarité décrites dans mon billet sont obtenues dans des isolats différents (il n’y en pas 2 dans le même). Il n’y a donc pas lieu dans combiner les probabilités. Le calcul que nous venons de faire n’est qu’une très grossière approximation qui ne tient pas compte du fait que les lettres A,T,G,C ne sont pas en proportion identiques et que les séquences naturelles se composent de « mots » de 3 lettres (codons) qui ne sont pas équiprobables, ni la fréquence de leur juxtaposition. Enfin, l’évolution naturelle amène des virus totalement différents à réutiliser des motifs de séquences qui se ressemblent car ils codent des fonctions essentielles. Le calcul rigoureux est obtenu au terme d’un modèle statistique et de calcul de probabilités très complexe que seuls des lecteurs très avertis pourront consulter utilement (doi: 10.1073/pnas.87.6.2264). L’espérance mathématique calculée rigoureusement a une valeur de 3.8. Les ressemblances détectées entre le SARS-CoV2 et HIV ne sont donc pas « significatives » d’une manipulation génétique.
  
  Répondre
Socrates
21.04.2020 13h37

Il serait intéressant de savoir quelle protéine contient la chaîne peptidique CANFNVLFSTVF et sa fonction virale. Il y a peut-être des similitudes dans certaines étapes virales pour différents virus, ce qui nécessite des séquences similaires des codons.

Réagir
Socrates
21.04.2020 15h27

Merci beaucoup pour votre analyse probabilistique. En comparant les deux séquences, on trouve quatre codons différents : GTT/ GTA (Valine), TTA /TTG (Leucine), TTC /TTT (Phénylalanine) et ACA/ A-A (Thréonine ?). Par hasard, trois de ces codons (redondants) codifient les mêmes acides aminés, tandis que le quatrième n’est pas clair. Je me demande aussi pourquoi le premier codon sélectionné dans la séquence est le codon TGT et pas ATT, ce qui aurait donné une chaîne peptidique IVQTLMFYSLQCS pour le CoV-2 et MVQILFYSAQ(?)CS pour le HIV, donc complètement différente. J’ai aussi remarqué, en commençant par la première lettre, la présence du codon ATG en 6ème position pour le CoV-2 et en 1ère position pour le HIV, qui pourraient être des sites d’initiation et dans ce cas il faudrait commencer à comparer les deux séquences à partir des codons ATG, ce qui donne des chaines peptidiques complètement différentes pour les deux virus. Merci d'avance pour votre commentaire.

Réagir
FredericN
22.04.2020 10h48

Bonjour
Merci pour vos éclaircissements qui sont très appréciés.
Je comprends tout à fait que le tirage statistique aléatoire avec 1 chance sur 4 n’est qu’une approximation, mais il a le mérite d’être facilement illustratif et c’est pourquoi je pense que c’est une bonne idée que vous l’ayez utilisé dans cet article.
A l’exception des nouvelles informations que vous indiquez (nombre de nucléotides à prendre en compte), il me semble que mon calcul initial tenait bien compte des points que vous indiquez dans votre réponse.
Si l’on considère le résultat 33/38, la première proba P1 était la chance de pouvoir trouver à l’identique une chaine de 38 lettres issue du HIV dans le Covid.
Cette proba allait ensuite être corrigé en P2 par le fait que 5 lettres étaient erronées, afin de donner le 33/38 que vous indiquez.
P1 peut se considérer comme la proba de tirer 38 lettres exactes d’affilé (1/4 exp 38, que je vais noter comme vous 1/4^38), avec autant de résultats acceptables que l’on peut découper le Covid en chaines de 38 lettres (on peut surestimer cela en supposant que ce nombre = nombre de nucléotides du Covid), et avec autant de tirages que l’on peut découper le VIH en chaines de 38 lettres (on peut surestimer cela en supposant que ce nombre = nombre de nucléotides du VIH).
P1 = (1/4^38) x Nbre nucleotide Covid x Nbre nucleotides HIV
P2 corrige P1 en tenant compte qu’il y a 5 lettres erronées. Ces dernières peuvent se trouver partout dans la séquences de 38 lettres mais sont interchangeables (C(38, 33) ≈ 5x10^5, meilleure notation que ce que j’indiquais par 38*37*36*35*34/(5*4*3*2)). Il faut d’autre part pour ces 5 lettres faire sauter la contrainte d’être exacte donc on multiplie par 4^5
Au final : P2 = P1 x C(38,33)x4^5 = (1/4^33) x 5x10^5 x Nbre nucleotide Covid x Nbre nucleotides HIV
En utilisant : Nbre nucleotide Covid = 30 000 et Nbre nucleotides HIV = 9200, on trouve : P2 = 1.9*10^-6, soit moins de 2 chances sur 1 million.

Si je prends les nouveaux chiffres que vous indiquez :
Nbre de nucléotides à prendre en compte sur SARS-CoV2 : 60 000 (et non 30 000), soit 2 fois plus.
Nbre de nucléotides à prendre en compte sur HIV : 100 000 (et non 9200), soit 10 fois plus
On arrive à P’2 = P2 x 20 = 4 chances sur 100 000, et cela pour la seule séquence 33/38.

Du fait que l’on prend en compte 100 000 nucléotides pour le HIV, il me semble que l’on peut multiplier les proba 33/38 et 28/30, ce qui diminue encore cette proba par à peu près le même nombre ?
Merci de vos retours.

Réagir